Bire bir fonksiyon nedir? Matematikteki önemli kavramlardan biri olan bire bir fonksiyonlar, belirli bir giriş değerinin yalnızca tek bir çıkış değerine karşılık geldiği özel bir fonksiyon türüdür. Bu makalede, bire bir fonksiyonların 10 temel özelliğini keşfedeceksiniz. Her bir özellik, bire bir fonksiyonların matematiksel yapısını ve uygulamalarını anlamanızı sağlayacak detayları içermektedir. Okuyucular, bu liste aracılığıyla bire bir fonksiyonların neden bu kadar önemli olduğunu ve çeşitli matematiksel bağlamlarda nasıl kullanıldığını öğrenme fırsatı bulacaklar. Göz atmaya hazır mısınız?
İçerik Tablosu
- 1) Bire bir fonksiyonun tanımı: Her bir elemanın benzersiz eşleşmesi.
- 2) Tanımlama aralığı: Fonksiyonun tanımlı olduğu küme.
- 3) Görüntü kümesi: Fonksiyonun ulaştığı değerler kümesi.
- 4) Ters fonksiyon: Bire bir fonksiyonun tersini elde etme.
- 5) Bire birlik şartları: İki farklı elemanın farklı görüntülere sahip olması.
- 6) Grafiksel gösterim: Bire bir fonksiyonun grafiksel olarak analizi.
- 7) Uygulama alanları: Matematik ve bilimde bire bir fonksiyonların önemi.
- 8) Matematiksel örnekler: Bire bir fonksiyona örnekler ile açıklama.
- 9) Bire bir fonksiyonların önemli özellikleri: Analiz ve uygulamalardaki rolleri.
- 10) Bire bir fonksiyonların eğilimleri: Fonksiyonun büyüme ve azalma davranışları.
- Sık Sorulan Sorular
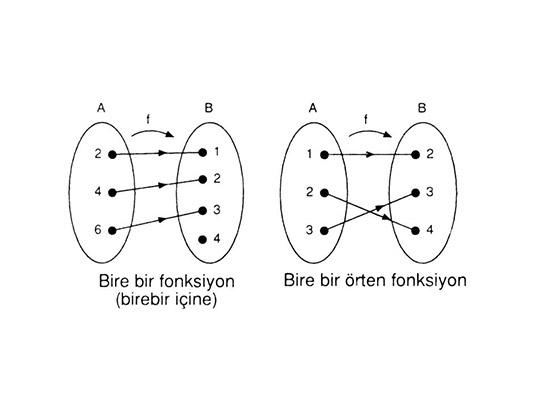
1) Bire bir fonksiyonun tanımı: Her bir elemanın benzersiz eşleşmesi
Bire bir fonksiyon nedir? sorusu, matematik dünyasında sıkça karşımıza çıkan bir kavramdır. İsterseniz bunu bir arkadaş toplantısındaki ikramlıklara benzetelim. Herkesin bir çerezi, bir tatlıyı olduğu gibi, bire bir fonksiyonda da her bir girdi (x) için bir çıktı (y) vardır ve bu çıkıtlar birbirine özeldir.Yani, her insanın bir tatlısı, her x’in de bir y’si vardır. Bu eşleşme, matematiksel bir denge oluşturur ve birçok uygulamada önemli bir rol oynar.
Benzersizlik ve Eşleşme
Eğer bir fonksiyon bire birse, bu altında yatan en temel özellik, her girdinin (x) benzersiz bir çıktı (y) ile eşleşmesidir.Başka bir ifadeyle, hiç kimsenin tatlısı başkasına ait olamaz.Üzerinde “benim” yazan bir çerez daha olamaz! Bu durum, grafiksel olarak bir doğrusal fonksiyonun her x’in, yalnızca bir y ile eşlemesi olarak görülür. Düşünün ki, bir fotokopi makinesi bir kopya çıkarırken yalnızca bir kopya verir. Başka adımda geri dönüp tekrar fotokopi çekmeye kalktığınızda, bu sadece o tek bir kopyanın aslına benzer başka bir versiyonu olabilir.
Günlük Hayatta Bire Bir Fonksiyon
Bire bir fonksiyonun günlük hayatımıza ne kadar entegre olduğunu hiç düşündünüz mü? Mesela,bir arkadaş grubunda herkesin bir başka arkadaşla oynadığı bir oyunda,herkesin sadece bir partneri vardır,ve bu partnerlik durumu eşsizdir. Bu tür müsabakalarda, bire bir eşleşme sayesinde kimse dışarıda kalmaz ve herkesin bir partneri olur. Aynı şey bire bir fonksiyonlarda da geçerli; her elemanın eşleşmesi, sistemdeki düzeni sağlar.
Özellikler ve Faydalar
- Benzersizlik: Her X, yalnızca bir Y ile eşleşir; bu da sistemin düzenli ve öngörülebilir olmasını sağlar.
- İleri Geri İşlemler: Bire bir fonksiyonlar, tersine çevrilebilir; bu da matematiksel hesaplamaları kolaylaştırır.
- Uygulama Esnekliği: Bire bir fonksiyonların birçok alanda kullanım imkanı vardır; bilgisayar bilimleri, mühendislik ve veri analizi gibi.
bir bire bir fonksiyon varken, ilişkilerimizdeki karmaşıklığı çözmek için gereken şeffaflık sağlanır. Matematiksel modeller ve teoriler, bire bir fonksiyonlar aracılığıyla netleşir ve sonuçların güvenilirliği artar. bu sayede kullanıcılar,çeşitli uygulamalarda daha sistematik bir yaklaşım geliştirebilirler.
Sonuç olarak, bire bir fonksiyonların yalnızca matematikte değil aynı zamanda ilişkilerimizde ve günlük yaşamımızda da önemli bir yer tuttuğunu fark etmemiz gerekiyor. Siz bir bire bir fonksiyon gibi eşleşmelerde nasıl bir düzen oluşturuyorsunuz? Ya da çevrenizdeki bireylerin birbiriyle olan ilişkilerinde hangi özellikleri gözlemliyorsunuz? Yanıtlarınız, bire bir fonksiyonların ne kadar değerli olduğunu daha iyi anlamamıza yardımcı olabilir.

2) Tanımlama aralığı: Fonksiyonun tanımlı olduğu küme
Bire bir fonksiyon nedir? Bu sorunun cevabını bulmak için önce konuya eğilmemiz gerekiyor. İlk olarak, fonksiyonun tanımlı olduğu kümeden başlamak iyi bir fikir. Tanımlama aralığı, bir fonksiyonun üzerinde işlem yapabileceği değerlerin toplamını ifade eder. Yani, bir bire bir fonksiyon için bu değerler ne kadar çeşitliyse, fonksiyonun sağladığı sonuçlar da o kadar zengin olur. Peki, biz bu zenginlikten hangi yollarla yararlanabiliriz?
- Çeşitlilik ve Seçenekler: Tanımlama aralığı, bire bir fonksiyonun haritasını oluşturur.Örneğin, bu fonksiyon yalnızca belirli bir aralıktaki değerleri alıyorsa, yeni buluşlar ve çıkarımlar yapmak için yeterli materyale sahip olmayabiliriz. Karar verme sürecinde çeşitliliğin ne kadar önemli olduğunu hiç düşündünüz mü? Örneğin, bir alışverişte karşımıza çıkan seçenekler arasında sıkışıp kalınca, gerçekten neye ihtiyacımız olduğunu gözden kaçırabiliriz. Bu bağlamda, fonksiyonların tanımlama aralığı bize daha fazla seçenek sunar.
- Fonksiyonel İletişim: Düşünün ki bir bire bir fonksiyon, iki kişi arasındaki özel bir iletişim gibidir. Bu iletişimde her iki taraf da birbirini anlar, böylece bilgi akışı sağlıklı bir şekilde gerçekleşir. Tanımlama aralığı, bire bir fonksiyonlar için bu iletişimi daha etkin ve eksiksiz hale getirir.Belki de sevdiklerinizle yaptığınız anlam dolu sohbetleri hatırlarsınız. Her kelimenizin bir karşılığı vardır; anladığınızdan emin olduğunuz için iletişiminiz sürekli canlı kalır.
- İnovasyon ve Yaratıcılık: Her bir tanımlama aralığı, bire bir fonksiyonların önceki çizgilerinin dışına çıkmasını sağlayabilir. Bir yazım sürecindeyken,farklı fikirlerin etrafında dönmek sıkıcı bir durum olabilir. Ancak, tanımlı bir aralık içinde çeşitli noktaları keşfettiğinizde, özgün ve yaratıcı çözümler bulma olanağınız artar. Bu, matematikte olduğu kadar günlük yaşamda da geçerli. Siz de bazen dar bir alanda kalıp yeni fikirlere ulaşmada zorluk mu yaşıyorsunuz?
- Veri Yönetimi ve Analiz: Özellikle günümüzü etkileyen veri çağında, tanımlama aralığı bire bir fonksiyonlar için veri yönetimi açısından büyük bir öneme sahiptir. Verilerin sınıflandırılması, hangi alanların daha ileri analizler gerektirdiği konusunda hem belli bir struktur sunar hem de daha anlamlı sonuçlar elde etmenizi sağlar. Bir sıkıntıyla karşılaştığınızda, durup verilerinizi hangi aralıklara yayabileceğinizi düşünüyor musunuz? Bu düşünce tarzı, problemleri çözme yolu olarak oldukça faydalı olabilir.
- Geçiş Dönemleri: Hayatımızda geçiş dönemleri yüzyıllardır süregelen büyük bir dönüşüm kaynağıdır. Örneğin, bire bir fonksiyonlar da bu dönüşümdeki kırılma noktalarını belirleyebilir. Fonksiyonun tanımlama aralığı, gelecekteki geçişler için kritik öneme sahip olabilir. Hayatınızın dönüm noktalarını hatırlıyor musunuz? İşte bunlar da matematikteki tanımlama aralıklarının sunduğu olasılıklara benzer şekilde, insan yaşamında sürekli alternatif yaratır.
Bire bir fonksiyon nedir sorusuna tanımlama aralığı perspektifinden baktığımızda, yalnızca matematiksel bir kavram olarak kalmadığını; bunun yanında günlük yaşamınıza, karar verme süreçlerinize, iletişiminize ve yaratıcı düşünme biçiminize de ışık tutabileceğini görebiliriz. Peki, siz bu konudaki deneyimlerinizi bir başkasıyla paylaşmaya ne dersiniz?
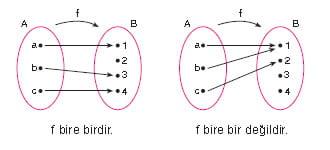
3) Görüntü kümesi: Fonksiyonun ulaştığı değerler kümesi
Görüntü Kümesi: Fonksiyonun Ulaştığı Değerler Kümesi
Bir fonksiyonun görüntü kümesi,onun ulaştığı değerlerin toplamını temsil eder. Bu terim ilk duyulduğunda karmaşık gelebilir, ancak aslında son derece doğaldır. Hayatımızda her gün benzer olayları deneyimliyoruz; mesela, bir restoranın sunduğu menüdeki yemekler gibi. her lokantanın sunduğu yemekler farklıdır, ve sizin de mevcut yemeklerden hangisini seçeceğiniz tamamen sizin damak tadınıza bağlıdır. Aynı şekilde, bir bire bir fonksiyonun her girdisi, kesin olarak bir çıktıyla eşleşir; dolayısıyla, bu çıktılar görüntü kümesini oluşturur. Peki,sizce hangi durumlarda bir fonksiyonun görüntü kümesi sizi en çok etkiler?
Görüntü kümesinin en öncelikli özelliklerinden biri,her elemanın yalnızca bir kez görünmesidir. Bu durum, bire bir fonksiyonların en belirgin özelliklerinden biridir. Aklınıza gelen herhangi bir bire bir fonksiyonu düşünün; mesela, cüzdanınızdaki para. Her bir kuruşun belirli bir yere tahsis edildiğini varsayıyorum! Hiç de olsa, 1 TL’nin iki farklı yere dağılması söz konusunu bile olamaz. Bu sebeple, görüntü kümesi her defasında benzersiz değerler sunarak bize net bir sonuç sağlar. Sizce bu durum, bire bir fonksiyonları neden önemli kılar?
Bir diğer dikkat çekici özellik, görüntü kümesinin ilgili değere en kısa yoldan ulaşabilmesidir. Hayatın pek çok alanında olduğu gibi, en kısa yolu tercih etmek her zaman en mantıklısıdır. Örneğin, bir yolculuk yaparken en kısa rotayı seçmek, vaktinizi verimli kullanmanızı sağlarken, aynı zamanda daha az enerji harcanmasına da yardımcı olur.Bire bir fonksiyonlar da benzer bir mantıkla çalışır; her elemanı yalnızca bir kez kullanarak net ve doğru sonuçlar elde etmeyi sağlar. O halde, sizin için en kısa yol hangisi?
Ayrıca, görüntü kümesinin faydası, çeşitli grafiklerde ve işlevlerde görselleştirme sağlamasıdır. Fonksiyonları grafik üzerinde incelediğinizde, görüntü kümesinin sunduğu değerleri görmek, matematiksel ilişkilerin daha net ortaya çıkmasına yardımcı olur. Bunun yanı sıra, öğrenme sürecindeki çocuklar ve öğrenciler için görsel materyaller oluşturmak öğrenmeyi kolaylaştırır. Bir grafik ya da tablo üzerinde fonksiyon değerlerini izlemek, insanlara daha iyi anlama fırsatı sunar. Chefs’ table dizisini izlerken bir aşçının özel bir tarif oluşturma sürecine dair düşündüğünüzde, acaba o tarifin görüntü kümesi nedir?
Görüntü kümesinin daha geniş perspektifte sağladığı faydalara baktığımızda, matematik, mühendislik ve bilimsel hesaplamalar gibi birçok alanda büyük önem taşıdığını görebiliriz. Analiz yapmak veya bir problemi çözmek gerektiğinde, görüntü kümesine göz atmak bazen kritik bir karar alma sürecinde belirleyici olabilir. Her bire bir fonksiyonu,ona ait bir görüntü kümesi tarafından desteklenerek işler; bu yüzden,bu kavramı anlamak bize çok büyük yarar sağlayabilir. Sizce bir bire bir fonksiyonla bu görüntü kümesi bağlamında gelecekte nasıl bir katkı yapabilirim?
Tüm bu nedenlerden ötürü,bire bir fonksiyonların görüntü kümesi vasıtasıyla sağladığı özellikler,sadece matematiksel bir kavram olarak kalmayıp,günlük yaşantımızın içinde karşımıza çıkan önemli bir olgu haline dönüşür. Ancak yine de her bire bir fonksiyonun sunduğu görüntü kümesi, kendi potansiyelimiz ve deneyimlerimiz doğrultusunda şekillenir. Siz de bu konuyu daha derinlemesine düşünerek, kendi hayatınızdaki bire bir fonksiyonları ve görüntü kümelerini keşfetmeye ne dersiniz?
4) Ters fonksiyon: Bire bir fonksiyonun tersini elde etme
Bire bir fonksiyon, matematikte oldukça özel bir yere sahiptir. Bu fonksiyonlar, her bir girdi değerinin (girdi kümesindeki her bir eleman) bir ve yalnızca bir çıktı değerine (çıktı kümesindeki bir eleman) karşılık geldiği fonksiyonlardır. İşte bu eşsizlik, bire bir fonksiyonları karşılaştırmalı olarak daha değerli kılar. Ters fonksiyon, işte bu bire bir fonksiyonların önemli özelliklerinden biridir. Hadi bunun üzerine bir derinlik kazandıralım!
Ters Fonksiyon Nedir?
Bire bir bir fonksiyonun tersini almak, yani bir çıktı değerinden (Y) girdiyi (X) bulmak demektir. Yani eğer f(X) = Y ise, ters fonksiyon f⁻¹(Y) = X olur. Buradaki anahtar kelimemiz “bire bir fonksiyon nedir?” sorusunu tam da bu noktada gitgide daha anlamlı hale getirir. İyi düşünün! Kendi hayatınızdaki bir durum var mı? Örneğin, bir arkadaşınıza bir mesaj attığınızda, o da aynı şekilde size cevap veriyorsa, bu bir ters fonksiyon gibidir! Ters ilişkiler hayatımızın her alanında.
Bire Bir Fonksiyonların tersini Elde Etmenin Faydaları
Bire bir fonksiyonların terslerini hesaplamanın birçok avantajı var.İlk olarak, bilgi akışının tersine çevrilmesi, çeşitli uygulamalarda işleri kolaylaştırabilir. Örneğin, bir anket verisi topladıysanız, kullanıcıların kimliklerini belirleyerek onları sıralamak istersiniz. Ters fonksiyonlar sayesinde,çıktılar üzerinden girdilere ulaşmak daha pratik hale gelir.Bu durum,verilerin analizi ve anlamlandırılması sırasında zaman kazandırır.
Bir diğer fayda ise, veri bütünlüğü ve doğruluğunun sağlanmasıdır. Özellikle veri tabanları ve yazılım uygulamalarında, ters fonksiyonlar kullanılarak, hatalı girişlerin tespit edilmesi mümkündür. Hatalı veri kaydı girişlerinin düzeltilebilmesi, sistemin güvenilirliğini artırır. Yani, bir bire bir fonksiyon ile başladıktan sonra, o fonksiyonun tersine gitmek bu bütünlüğü sağlamak açısından son derece değerlidir.
Kullanıcı Deneyimi ve Uygulamaları
Bire bir fonksiyonların tersleri, kullanıcı deneyimini de olumlu yönde etkiler. Sıkça rastladığımız bir durumu ele alacak olursak: Bir web sayfasında aradığınız bir ürün ya da bilgiye ulaşmaya çalışıyorsunuz. Eğer sayfa, kullanıcı etkileşimini dikkate alarak, bir ters fonksiyon gibi çalışıyorsa, yani girilen bilgilere göre doğru sonuçları rahatlıkla getirebiliyorsa, kullanıcı memnuniyeti bu durumdan doğrudan etkilenir.
Hemen düşündüğünüzde, internet siteleri ne kadar “kullanıcı dostu” olursa, o kadar da başarılı olurlar değil mi? Kullanıcı deneyimini geliştirmek ve olası hataları minimuma indirmek için, bire bir fonksiyonların terslerinden yararlanmak kesinlikle kaçınılmazdır.
Sonuç: Bire Bir Fonksiyonların Tersini Kullanmanın Önemi
Son olarak, bire bir fonksiyonlarının tersleri, matematiksel kavramlardan çok daha fazlasıdır; hayatımızın karşılıklı ilişkilerinin birer yansıması gibidir. Hayatınızda bu tür karşılıklı ilişkileri düşündüğünüzde, sosyal çevrenizde ya da iş yerinde fark ettiğiniz benzer durumlar olacak mı? Unutulmaması gereken, bire bir fonksiyonlar sadece matematiksel bir kavram değil, aynı zamanda insan ilişkilerindeki derinliği de ifade eder.
Belki de bire bir fonksiyonların tersini anladığınızda, toplumsal ilişkilerinizde bile bir keskinlik ve netlik kazanabileceğinizi keşfedeceksiniz! Matematiksel yapıların hayatımıza etkisini bir düşünün, ve belki de bir bire bir fonksiyon üzerinden kendinize sorular sorarak, yeni ilişkilere kapı aralayabilirsiniz!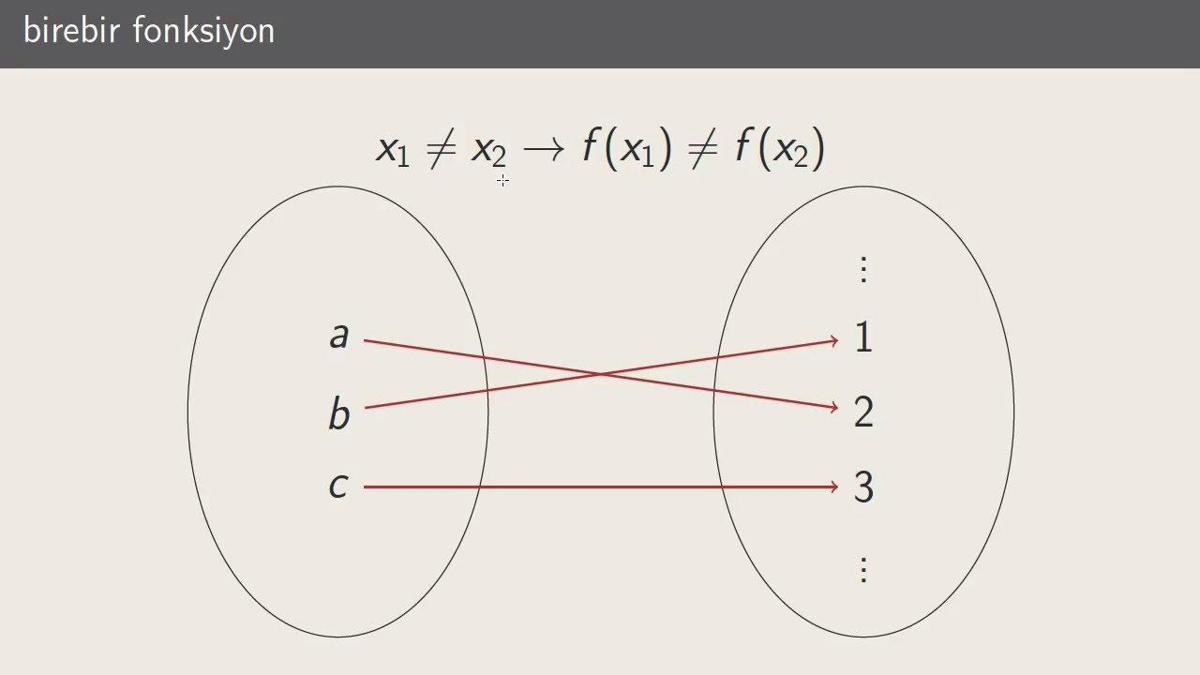
5) Bire birlik şartları: İki farklı elemanın farklı görüntülere sahip olması
Bire bir fonksiyon nedir sorusu, matematiksel bir yolculuğa çıkmak isteyenler için oldukça önemli bir başlangıçtır. Bu terimde sıkça karşılaştığımız bire bir fonksiyonlar, her bir girdinin eşsiz bir çıktıyla buluşmasını sağlar. Ama biliyor musunuz, bu sadece matematikte değil, hayatın birçok alanında da karşımıza çıkan bir kavram? Örneğin, her insanın birbirine benzemeyen parmak izleri gibi düşünün. İşte bire bir fonksiyonu anlayabilmek için bu “bire birlik” şartları önemli bir anahtar! İki farklı elemanın farklı görüntülere sahip olmasının perde arkasına bakalım.
- Seçim Süreci: Bire bir fonksiyon, bir nevi seçim yapmak gibidir. Herhangi bir grup içinde, her bir bireyin farklı bir rengi, boyu veya kişiliği olduğunu düşünün. Eğer seçimlerinizi yaparken her bir bireyin kendine özgü bir hissettireceğini biliyorsanız, bu bire bir fonksiyon görüş açınızı da genişletebilir.Sınıf arkadaşlarınızdan birinin kahverengi gözleri olduğunu, diğerinin ise mavi olduğunu düşünün. Bu farklar,onların bire bir temsil edilmesini sağlar.
- Etki Alanları: Kimse birbirinin kopyası değil, öyle değil mi? İşte buna bire bir fonksiyon diyoruz. Her bir elemanın çıkış noktalarının birbirinden farklı olması, farklı sağladığı sonuçları doğurmuş olur. Bu durum, özellikle dijital dünyada, veri tabanlarındaki kullanıcıların her birinin kendine özel bilgileri olması açısından oldukça önemlidir. Örneğin,sosyal medya hesaplarınızda herkesin kendine ait bir kullanıcı adı olması gibi. Bu, kimliklerinizi ve kişisel verilerinizi güvence altına alır.
- Farklılık ve Zenginlik: Bire bir fonksiyonun sağladığı en önemli yararlardan biri de çeşitlilik. Farklı göz renkleri gibi, farklı elemanlar farklı sonuçlar doğuracağından, bu durum zenginliğe yol açar. hayatın her alanında olduğu gibi, farklı bakış açılarının beni, seni ve diğerlerini zenginleştirdiğini düşünüyor musun? Bu bire bir özellik ile insanlar birbirine olan anlayış ve iletişimini de güçlendirebilir.
- Kontrol ve Güvenlik: Bire bir işlemlerde, her elemanın kendine ait bir görüntüsü olduğu için kaybolma, benzerlikten kaynaklanan yanlış anlaşılmalar veya bilgi sızıntıları en aza indirilir. Bir nevi matematiksel güvenlik sistemi denebilir! Bu, aynı zamanda çeşitli sektörlerde organizasyonların düzenli ve hafızalı bir şekilde çalışmalarına da yardımcı olur. Bir bankada her müşterinin sadece kendi hesap bilgileri olması, bu güvenliği simgeler.
Bire bir fonksiyon nedir sorusunun deryasında kaybolmamak için bu bire birlik şartlarının hayatımıza sağladığı faydaları göz önünde bulundurmak gerçekten önemli. Bire bir fonksiyonların işleyişinin sadece matematikle sınırlı olmadığını,aynı zamanda toplumumuzun bireyselliği ve çeşitliliğiyle yakından ilgili olduğunu unutmayın. Son olarak, sizin için önemli olan başka hangi birebir örnekler var? Düşünmeden geçmeyin, çünkü farklılıklarımız bizleri zenginleştirir!
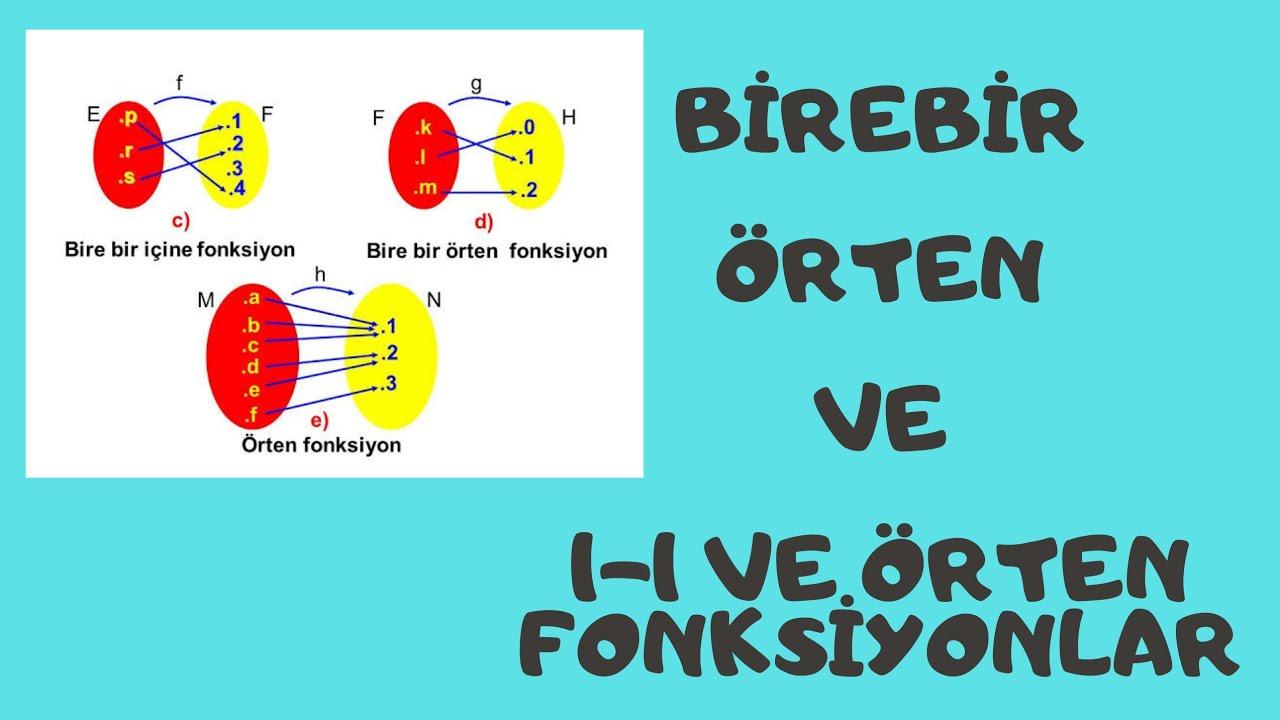
6) grafiksel gösterim: Bire bir fonksiyonun grafiksel olarak analizi
Grafiksel analizin önemi
Bire bir fonksiyon nedir sorusunu yanıtlamanın en etkili yollarından biri, onun grafiksel gösterimini incelemektir. Hayal edin ki bir parkta yürüyüş yapıyorsunuz ve birisi size “Bu yol hangi yönlere gidiyor?” diye soruyor. O zaman karşınızdaki manzaranın kadar önemli! Grafikler de bu şekilde matematiği daha görsel ve anlaşılır hale getiriyor.Bire bir fonksiyonun grafiğini yorumlamak ise, anlamayı kolaylaştırıyor. Grafiği nasıl okuduğunuz, fonksiyonun davranışını anlamanıza yardımcı olur.
Birbiçim ve Yükselti Analizi
Bire bir fonksiyonların grafikleri her zaman eğridir ve bu grafiklerde her x değeri, yalnızca bir y değerine karşılık gelir. Grafik üzerinde bir çizgi çektiğinizde, bu çizgi yalnızca bir noktadan geçiyorsa, o fonksiyon bire birdir. Düşünün ki bir kafede oturuyorsunuz ve arkadaşlarınız farklı masalarda oturuyor. Eğer her masada sadece bir kişi varsa, işte tam da bu bire bir ilişkidir! Grafiklerle çalışırken, bu ilişkiyi görselleştirmek, matematiksel soyutlamaları kavramanızı inanılmaz derecede kolaylaştırır.
Fonksiyonel Davranışlar
Bire bir fonksiyonun grafik kısmı, bize fonksiyonun sürekli mi, kesikli mi, ya da artan mı azalan mı olduğunu gösterir. Daha önce bir pazar gezmiş olabilirsiniz. Manavda meyveleri seçerken, seçimlerinizin tatlı mı ekşi mi olduğu gibi, grafikler de fonksiyonun davranışlarını anlamanıza yardımcı olur. Örneğin, bir fonksiyonun grafik üzerinde artan bir eğim göstermesi, onun sürekli ve bire bir bir yapı içerdiği anlamına gelir. Siz de grafiklere bakarak kendi hayatınızdaki kararları nasıl aldığınızı düşünmeye başlayın; seçimlerinizin hangi yönlere yöneldiğini kolayca görebilirsiniz.
Kullanıcı Deneyimi ve Grafik Analizi
Grafikler aynı zamanda kullanıcı deneyimini artırmanın mükemmel bir yoludur.Duygularımızı ve düşüncelerimizi ifade etmenin birçok yolu var ama bir grafin sunduğu görsellik tartışmasız etkileyicidir. Siz hiç bir grafiği incelediğinizde hissettiğiniz duyguları düşündünüz mü? Bir kere daha bakın; belki de beğendiğiniz bir eğriyi ya da kesişim noktasını gördüğünüzde içten bir mutluluk hissediyorsunuzdur! Grafikler, bire bir fonksiyon nedir konusunu aydınlatmanın yanı sıra, bizlere görev ve sorumluluklarımızı nasıl organize edebileceğimiz konusunda ipuçları verir.
Görselleştirme Araçları ve İstatistiksel Destek
Son olarak, bire bir fonksiyonun grafiksel analizi, birçok görselleştirme aracı ile desteklenmektedir.Örneğin, Python ile Matplotlib gibi kütüphaneler kullanarak grafikler oluşturmak, bire bir fonksiyonları keşfetme açısından oldukça eğlenceli bir deneyim sunar. Sizler de bir gün bu tür araçlarla oynamayı deneyin; örnek veriler kullanarak eğrileri oluşturmak, grafik analizi ile bire bir fonksiyon nedir sorusunun yanıtını bigger picture’a taşıyacaktır. unutmayın,grafik analizi yaparken yanlış bir çizim yapmaktan korkmayın; her hata,yeni bir öğrenme fırsatıdır!
7) uygulama alanları: Matematik ve bilimde bire bir fonksiyonların önemi
Uygulama alanları: Matematik ve bilimde bire bir fonksiyonların önemi
Bire bir fonksiyon,matematikte her elemanın bir diğerine karşılık geldiği,yani her çıktının yalnızca bir girdi ile ilişkili olduğu durumları tanımlar. Bu, sadece gözle görünür bir kavram değil, aynı zamanda günlük yaşamda birçok alanda karşımıza çıkar. Peki, çoğu insanın belki de karşılaştığı ama üzerinde çok düşünmediği bu kavram neden bu kadar önemli? İşte bire bir fonksiyonların uygulama alanlarından birkaç örnek!
- Veri Şifreleme: Dijital dünyanın temel taşlarından biri olan şifreleme yöntemleri, bire bir fonksiyonları sıkça kullanır. Mesela, bir şifreleme algoritması oluşturulurken, her karakterin başka bir karakterle eşleşmesi gerekir.Bunun doğru yapılması, verilerin güvenliğini sağlamak için kritik öneme sahiptir. Sizce dijital verilerimizin güvenliği için bire bir fonksiyonlar olmadan bir şansımız kalır mıydı?
- Matematiksel Modelleme: Bilim insanları, biyolojik sistemlerden ekonomik modellere kadar pek çok alanda bire bir fonksiyonlarla çalışır. Örneğin, bir ekosistem modelinde her türün diğer türlerle olan etkileşimi bire bir fonksiyonlarla ifade edilebilir. Böylece karmaşık sistemleri daha iyi anlayabiliriz. Siz de karmaşık bir durumu bire bir fonksiyonlarla çözmeye çalıştığınızda neler hissettiniz?
- Veritabanı Yönetimi: Veritabanlarında, bire bir ilişkiler verilerin düzenlenmesi ve erişimi için kritik öneme sahiptir. Kullanıcı bilgileri gibi benzersiz veriler, diğer tablolarda karşılıkları olmadan saklanır. Bu durum, veri bütünlüğünü sağlarken aynı zamanda sorgulamaları da hızlandırır.Sizin için en verimli veri düzenleme yöntemi hangisi? Belki de bire bir ilişkilerle tanışmanız gerekiyordur!
- İletişim ve Ağ Kurma: Sosyal ağlarda, bire bir ilişkiler iletişim akışını güçlendirir. Her kullanıcının yalnızca bir profili olduğunda, karşılıklı iletişim ve etkileşim daha anlamlı hale gelir. Zaten sosyal medya üzerinden tanıştığınız birisiyle gerçek hayatınızda da bire bir bir iletişim kurmak zorunda kaldığınızda ne hissettiniz? İşte bu birbirinizi tanımanızın en güzel örneğidir!
- Eğitim ve Öğrenme Süreçleri: Öğrencilerin bire bir etkileşimi sayesinde, daha fazla öğrenme fırsatı doğar. Eğitimde bire bir yöntemlerle,öğretmenler her bir öğrencinin ihtiyacına özel çözümler sunabilir. Sınıf içinde bire bir etkileşimler yaşadığınızda, öğrenme konusundaki deneyimlerinizin nasıl değiştiğini düşünün.
Gördüğünüz gibi bire bir fonksiyonlar, birçok alanda hayatımızı etkileyen önemli unsurlar.Herhangi bir konuda şansımızı denemek ve bire bir ilişkilere dair düşünmek, belki de daha geniş bir perspektif kazanarak potansiyelimizi artırabilir.Sizce bire bir fonksiyonların sağladığı bu avantajları nasıl değerlendirebilirsiniz?
8) Matematiksel örnekler: Bire bir fonksiyona örnekler ile açıklama
Bire Bir Fonksiyon Nedir?
Bire bir fonksiyon, matematik dünyasında oldukça önemli bir kavramdır. Ama haydi, bunu biraz daha gündelik bir dille ve örneklerle açıklamaya çalışalım. Düşünsene, koca bir parti var ve herkesin elinde bir çiçek var. Ancak, partide ki herkes yalnızca bir çiçek alabilir! İşte bu, bire bir fonksiyonun kısaca bir özeti gibi. Yani, eğer bir eleman bir çıktıya karşılık geliyorsa, o çıkışın başka bir girdi tarafından aynı şekilde karşılanması mümkün değil!
- Örnek 1: Kişi ve Telefon Numarası - Her insanın kendine ait bir telefon numarası vardır. Eğer Ali’nin telefon numarası 555-1234 ise, aynı telefon numarası bir başka kişiye ait olamaz. Yani her kişi için bir telefon numarası, tam olarak bire bir bir fonksiyon oluşturur. Senin telefon numaran kim bilir, belki de herkesin hatırladığı o özel numaradır!
- Örnek 2: Öğrenci ve Not – Bir sınıfta her öğrencinin yalnızca bir notu vardır. Ali’nin notu 85, Ayşe’nin notu 90. İkisi de farklı notlara sahip. Bu da bire bir fonksiyon özelliğini gösterir! Peki, sen hangi notla gururlanmak istersin? Belki de yüksek notlar senin yeni doğrudan aklında!
- Örnek 3: Kitap ve yazar – Her kitap, yazarıyla ilişkilendirilmiştir. “Suç ve Ceza” kitabı Dostoyevski tarafından yazıldı, başka bir “Suç ve Ceza” kitabı yok. Her bir kitap, tek bir yazarla bire bir ilişki taşır. Yazar olmaya ne dersin? Zihnindeki hikayeleri kelimelere dökme zamanı gelmedi mi?
- Örnek 4: Eşya ve Renk – Hayatın içindeki objeler de bire bir ilişkilere sahiptir. Örneğin, mavi bir elbise yalnızca tek bir renge sahiptir, başka bir mavi elbiseyle yer değiştiremez. Hangi renkte elbiseyi daha çok seversin? Aklında en çok ne tür renkler var?
- Örnek 5: Film ve Yönetmen – Her film, onu yöneten bir kişi ile özdeşleşir. Steven Spielberg’in yönettiği bir film, başka bir yönetmene ait olamaz.sinemaya olan ilgin, hangi film ile başladı? Yönetmenlerin sihirini hissediyor musun?
Bire bir fonksiyonun Önemi
Şimdi bire bir fonksiyon kavramını anladıktan sonra, bu kavramın yaşamımızdaki rolüne dalalım. Örneğin, her bir eşyanın ve kişinin kendine özel bir referansı vardır. Bu,karmaşadan uzak,düzenli bir sistem oluşturur. Gerçek hayatta bu tür düzenler sağlanmadığında, işler çok karışır, değil mi?
Belki de bu yüzden bire bir fonksiyon kavramı, matematiksel düşünceleri geliştirmenin yanı sıra, bazen hayatta karşımıza çıkan sorunları çözmekte de yardımcı olur. Kişisel deneyimlerinde, sence hangi bire bir ilişkileri daha çok görüyorsun? Klasik bir soru, ama üzerindeki düşünmeye değer!
Sonuç olarak, bire bir fonksiyonun örnekleri, sadece teorik düzeyde değil, yaşamlarımızda da sık sık karşımıza çıkar. Belki de bugün, çevrendeki bire bir ilişkilerle daha çok bağ kurarak bu matematiksel kavramın derinliğini keşfetmek için bir fırsat bulursun!
9) bire bir fonksiyonların önemli özellikleri: Analiz ve uygulamalardaki rolleri
Bire bir fonksiyonlar, matematik dünyasında adeta birer özel elmas gibidir. Peki, bire bir fonksiyon nedir? Bu sorunun cevabı, birçok matematiksel kavramla ilişkilidir. Bire bir fonksiyonlar,her bir girdi için farklı bir çıktı üreten fonksiyonlardır. Yani bir fonksiyon eğer bire bir ise, farklı girdiler asla aynı çıktıya yol açmaz. Analiz ve uygulamalardaki rollerine bir bakalım.
Birinci Özellik: Benzersiz Girdiler ve Çıktılar
Bir bire bir fonksiyonu düşündüğünüzde, onun özel bir “kimlik kartı” taşıdığını hayal edebilirsiniz. Düşünün ki, bir partiye gidiyorsunuz ve her bir davetli sadece kendine özgü bir isimle davet edilmiş. İşte bu durum, bire bir fonksiyonların temel prensiplerini temsil ediyor. Farklı isimler, farklı insanlar ve dolayısıyla farklı deneyimler demek!
Bu noktada kendinize şu soruyu sorabilirsiniz: “Hayatımda hangi durumlar, bire bir fonksiyon mantığını yansıtıyor?” Örneğin, sosyal medya platformlarında paylaşımlarınızın birbirine karışmadığı anları düşünün. Herkesin kendine ait bir ses tonu ve tarzı vardır; bu durum matematiksel bir bire bir yapı oluşturur.İkinci Özellik: Ters Fonksiyonların Var Olması
Bire bir fonksiyonların bir diğer önemli özelliği, ters fonksiyonların varlığını sağlamasıdır.Yani, bire bir bir fonksiyonda her çıktı, bir girdi ile bağlantılıdır ve bu bağlantı kolaylıkla tersine çevrilebilir. Örneğin, bir adresi bilmek, o adrese ulaşmanızı sağlarken, o adrese ait olan birinin kim olduğunu bilmek de o kişiye ulaşmanızı sağlar.
Bir an için kendi hayatınızdaki bu durumu düşünün: Hangi durumlar, bir bilgiyi geri almanıza ya da geçmişte yaptığınız bir hatayı düzeltmenize olanak sağladı? Belki de geçmişte bir arkadaşınıza yazdığınız o özel mesaj, onunla olan ilişkinizi sorgulamanıza sebep olmuştur.
Üçüncü Özellik: Uygulama Alanları
bire bir fonksiyonların önemli özellikleri arasında, uygulama alanlarının genişliği de dikkat çekiyor. Matematikte olduğu kadar, bilgisayar bilimleri, ekonomi ve sosyal bilimler gibi alanlarda da bire bir fonksiyonların kullanımı oldukça yaygındır. Örneğin, veri analizleri sırasında bire bir ilişkiler kurarak, farklı veri noktaları arasında anlamlı bağlantılar kurabiliriz.
Burada kendinize sormak isteyebilirsiniz: “Veri analizlerinde bire bir ilişkilerin beni nasıl daha iyi sonuçlara yönlendirdiğini hiç düşündünüz mü?” Bir karar almak için verileri değerlendirdiğinizde, ne tür örüntüler ortaya çıkıyor?
Dördüncü Özellik: Güvenlik ve Şifreleme
Son olarak, bire bir fonksiyonların güvenlik alanındaki rolünü ele almak gerekir.Aslında birçok şifreleme yöntemi, bire bir fonksiyonlar temelinde geliştirilmiştir. Kullanıcıların bilgileri, yalnızca kendilerine ait ve başka kimse tarafından çözülemeyecek şekilde korunur.
Güvenliğin önemi üzerine düşünün: “Kişisel bilgilerinizi korumak adına ne kadar tedbir alıyorsunuz?” Bire bir fonksiyonların sunduğu güvenlik, kişisel verilerinizi bir kalkan gibi korur.
Bire bir fonksiyonlar, matematiksel temel kavramların ötesinde günlük yaşamda da karşımıza çıkan önemli yapılar. Bu yapıların rolleri, bizim düşünce tarzımızı şekillendirirken, aynı zamanda veri faaliyetlerimiz ve ilişkilerimiz üzerinde derin etkiler bırakmaktadır. Unutmayın ki, her bire bir fonksiyon, aslında kendine has bir hikaye barındırır.
10) Bire bir fonksiyonların eğilimleri: Fonksiyonun büyüme ve azalma davranışları
Bire bir fonksiyonların büyüme ve azalma davranışları,matematiğin ve günlük hayatın köşe taşlarından biridir. Birçok yapı içinde karşılaştığımız bu kavram,aslında yalnızca sayıların ve fonksiyonların oyunundan ibaret değildir; duygusal ve sosyal hayatımızda da bir hikaye barındırır. Hayatta “bir şeyin artması” veya “azalması” gibi durumlar üzerine düşünecek olursak, bire bir fonksiyonların bu dinamikleri ne denli etkili bir şekilde yansıttığını daha iyi görebiliriz. Peki,bire bir fonksiyonları anlamak sizde nasıl bir etki yaratıyor? Hadi gelin,biraz daha derinleşelim!
1. Bire Bir Fonksiyon Nedir? Öncelikle, bire bir fonksiyonların ne anlama geldiğini özellikle vurgulamak gerek.Bire bir fonksiyon, çıktı değerlerinin (yani fonksiyonun aldığı değerlerin) her zaman benzersiz olduğu durumları tanımlar. Yani, iki farklı girdi değeri asla aynı çıkış değerini elde edemez. Bu durum, aslında sizin de sosyal yaşamınızdaki ilişkilerinizi yansıtır: Herkesin birbirinden farklı ve özel bir yeri vardır, öyle değil mi? İşte bire bir fonksiyonlar da bu farklılığı matematiksel bir şekilde temsil eder.
2. Büyüme ve Azalma davranışları Şimdi bire bir fonksiyonların büyüme ve azalma davranışlarını inceleyelim. Büyüyen bir fonksiyona baktınız mı hiç? Grafiği yukarıya doğru bir kaç adım attığında, adeta hayata yeni bir segmente geçiş yapar gibi hissedersiniz. Bu tür durumlar, olumlu bir gelişme veya bir başarı hikayesi olabilir.Ancak unutmayalım ki her zaman bir iniş de vardır. Azalma göstergesi, tıpkı hayatınızdaki zorluklar gibi, bir şeylerin sona erdiğini veya yeni bir başlangıç yaptığınızı ifade edebilir. Sizce bir şeylerin sona ermesi,aslında yeni bir başlangıç mıdır? Bu tür sorular,bire bir fonksiyonların büyüme ve azalma dinamiklerini anlamak için oldukça önemlidir.
3. Kullanıcı Deneyimleri ve Olumlu Etkiler bire bir fonksiyonların analizi, hayatımızın birçok alanında ve özellikle iş dünyasında belirleyici bir rol oynar. Örneğin, bir web sitesinin kullanıcı deneyimini optimize etmek için, hangi bileşenlerin büyüdüğü ve hangi bileşenlerin azaldığı üzerine düşünmek gerekir. Yani, kullanıcı deneyimi bire bir fonksiyonların algılamasıyla ilişkilidir. Kullanıcı feedback’leri, bir büyüme veya azalma eğilimi gösterdiğinde, bu sizin için hayati bir öneme sahip olabilir. Peki, sizce kullanıcı deneyimlerinde en çok hangi faktörler büyüme ya da azalma etkisi yaratıyor?
4. Sonuç: Bire Bir fonksiyonlarla Geleceği Şekillendirmek Sonuç olarak, bire bir fonksiyonların büyüme ve azalma davranışlarını kavramak, yalnızca matematiksel bir analizden ibaret değildir; aynı zamanda kendi yaşamınızda aldığınız kararları da gözden geçirmenize yardımcı olur. Belki de bir bire bir fonksiyon gibi benzersiz bir kişiliğe sahipsinizdir ve hayatınızda anlam katacak birçok büyüme ve azalma fazı yaşarsınız. Peki, bu büyümeleri nasıl değerlendirebilir ve daha fazlasını sağlamak için neler yapabilirsiniz? unutmayın, matematik yalnızca sayılardan ibaret değildir; yaşamın kendisini de anlamaya yardımcı olan bir araçtır.
Sık Sorulan Sorular
Bire Bir Fonksiyon Nedir?
Bire bir fonksiyon, her bir elemanın yalnızca bir karşılığı olduğu ve her bir çıktının yalnızca bir girdi ile eşleştiği bir matematiksel fonksiyon türüdür. Bu, fonksiyonun herhangi iki farklı girdisinin mutlaka farklı çıktılar ürettiği anlamına gelir.Bire bir fonksiyonlar, matematiksel analizde, cebirsel yapıların incelenmesinde ve çeşitli uygulamalarda önemli bir rol oynamaktadır.
1. Bire bir fonksiyonun tanımı nedir?
Bire bir fonksiyon, her x elemanının yalnızca bir y elemanına karşılık geldiği bir fonksiyon tipidir. Yani, eğer f(a) = f(b) ise, bu durumda a = b olmalıdır. Bu özellik, bire bir fonksiyonun benzersiz bir eşleşme sağladığını gösterir.
2. Bire bir fonksiyonun özelliği nedir?
bire bir fonksiyon,şu temel özelliklere sahiptir:
- Herhangi iki farklı girdi için farklı çıktılar üretir.
- Fonksiyonun grafiği,yatay bir çizgi testi ile kontrol edildiğinde hiçbir noktada iki kez kesilmemelidir.
- Eşitlik durumu, yalnızca girdiler arasında geçerlidir.
3.Bire bir fonksiyonlar hangi matematiksel işlevlerde kullanılır?
Bire bir fonksiyonlar, matematiksel analiz ve cebir, istatistik, bilgisayar bilimi ve mühendislik alanlarında yaygın olarak kullanılır. Özellikle şifreleme sistemlerinde ve veri bütünlüğünün sağlanmasında önemli bir rol oynarlar.
4. Bir fonksiyonun bire bir olup olmadığını nasıl kontrol edebilirim?
Bir fonksiyonun bire bir olup olmadığını kontrol etmek için şu yöntemleri kullanabilirsiniz:
- Hedef kümedeki her elemanı bir kez kullanıp kullanmadığını kontrol edin.
- Fonksiyonun grafiğinde yatay çizgi testi uygulayın.
- Algebraik olarak, f(x1) = f(x2) eşitliğinin yalnızca x1 = x2 sonucunu verip vermediğini kontrol edin.
5. Bire bir fonksiyon ile bire çok fonksiyonu arasındaki fark nedir?
Bire bir fonksiyon, her eleman için benzersiz bir eşleşme sağlarken, bire çok fonksiyon aynı çıktıyı farklı girdilere karşılık gelen durumlarda kullanır.Bu, bire çok fonksiyonlar için birden fazla girdi ile aynı çıktıyı elde etme olasılığının olduğu anlamına gelir.
6. Bire bir fonksiyonların tersinin varlığı nedir?
Bire bir fonksiyonlar, ters fonksiyonları daima tanımlıdır. Eğer bir fonksiyon f bire bir ise, o zaman f’in ters fonksiyonu f^-1, her y elemanını bir x elemanına eşleştirir.
7. Bire bir fonksiyonların uygulama alanları nelerdir?
Bire bir fonksiyonlar, şu alanlarda önemli uygulamalara sahiptir:
- Veri madenciliği ve istatistiksel analiz.
- Şifreleme ve güvenlik sistemleri.
- Matematiksel modelleme ve optimizasyon problemleri.
8. Bire bir fonksiyonların oluşturulması ve örnekleri nelerdir?
Bire bir fonksiyon oluşturmak için, genellikle doğrusal olanlar tercih edilir. Örnekler:
- f(x) = 2x + 3
- f(x) = x^3
- f(x) = e^x
Her bir örnek, farklı x değerleri için farklı y değerleri üretir.
9. Bire bir fonksiyonların grafiksel temsilinin önemi nedir?
Fonksiyonların grafiksel temsili, bire bir olma durumlarını görselleştirir. Bu, fonksiyonun davranışını anlamayı ve analiz etmeyi kolaylaştırır.Yatay çizgi testi, bire bir fonksiyonu hızlıca belirlemenin etkili bir yoludur.
10. Bire bir fonksiyonların genel önemi nedir?
bire bir fonksiyonlar,matematiksel mantıklılık ve çözümleme süreçlerinde kritik bir rol oynar. Özellikle bilgi teorisi, şifreleme ve algoritmalar gibi alanlarda, verilerin doğru bir biçimde işlenmesi ve güvenli bir şekilde aktarılması için gereklidir. Bu yüzden, bire bir fonksiyonlar matematik ve uygulamalı bilimlerde vazgeçilmezdir.
Sonuç olarak, bire bir fonksiyon nedir sorusunun yanıtını anlamak, matematiksel kavramların daha derinlerine inmek için önemli bir adımdır. Yukarıda sıraladığımız 10 temel özellik, bire bir fonksiyonun matematikteki rolünü ve önemini daha iyi kavramanızı sağlıyor. Bire bir fonksiyonlar, her elemanın benzersiz bir görüntüye sahip olması ile özelliklerini belirler ve bu durum, matematiksel problemlerin çözümlenmesinde büyük avantajlar sunar.
Bu yazıda, bire bir fonksiyon kavramının yanı sıra, ilgili matematiksel terimleri ve uzun kuyruklu anahtar kelimeleri etkili bir şekilde kullanarak değinilen konuları derinlemesine inceledik. Bire bir fonksiyonların temel ilkelerini ve bunların önemini öğrenmek, matematik alanında daha ileri seviye çalışmalar yapabilmeniz için temel oluşturacaktır.
Bire bir fonksiyon üzerine bu bilgilendirici makalemiz umarız ki matematiksel düşünce yapınızı geliştirmiştir. Unutmayın ki, bire bir fonksiyonlar sadece teorik bir kavram değil, aynı zamanda pratik uygulamalarında da sıkça yer bulur.Matematik dünyasında daha fazla keşfe çıkmak ve bire bir fonksiyonlar hakkında daha fazla bilgi edinmek için içeriklerimizi takip etmeye devam edin.